Tangga jarak kosmos
Tangga jarak kosmos (Jawi: تڠݢ جارق كوسموس; juga dikenali sebagai skala jarak ekstragalaksi) adalah sesaran kaedah di mana para ahli astronomi menentukan jarak ke objek angkasa. Pengukuran jarak langsung sebenar objek astronomi mungkin hanya untuk objek yang "cukup dekat" (sekitar seribu parsek) ke Bumi. Teknik untuk menentukan jarak ke objek yang lebih jauh semuanya berdasarkan pelbagai korelasi yang diukur antara kaedah yang berfungsi pada jarak dekat dan kaedah yang berfungsi pada jarak yang jauh. Beberapa kaedah bergantung kepada lilin piawai, yang merupakan objek astronomi yang mempunyai kekilauan yang diketahui.
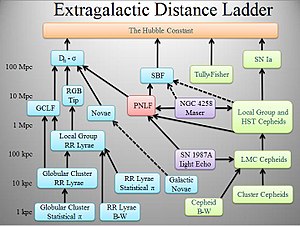
- Kotak hijau muda: Teknik yang digunakan untuk galaksi membentuk bintang.
- Kotak biru muda: Teknik yang digunakan untuk galaksi Populasi II.
- Kotak ungu muda: Teknik jarak geometri.
- Kotak merah muda: Teknik fungsi kekilauan nebula planet diterapkan kepada semua populasi Supergugus Virgo.
- Garis hitam padu: Langkah tangga yang ditentukur dengan baik.
- Garis hitam putus-putus: Langkah tangga penentukuran yang tidak menentu.
Analogi tangga timbul kerana tiada teknik tunggal yang dapat mengukur jarak pada semua julat yang ditemui dalam astronomi. Sebaliknya, satu kaedah boleh digunakan untuk mengukur jarak berdekatan, satu lagi boleh digunakan untuk mengukur jarak dekat dengan jarak perantaraan, dan sebagainya. Setiap langkah tangga menyediakan maklumat yang boleh digunakan untuk menentukan jarak pada tangga yang lebih tinggi seterusnya.
Pengukuran langsung
suntingPada dasar tangga adalah pengukuran jarak asas, di mana jarak ditentukan secara langsung, tanpa andaian fizikal mengenai sifat objek yang dipersoalkan. Pengukuran kedudukan bintang yang tepat adalah sebahagian daripada disiplin astrometri.
Unit astronomi
suntingPengukuran jarak langsung didasarkan pada unit astronomi (AU), iaitu jarak antara Bumi dan Matahari. Hukum Kepler memberikan nisbah yang tepat mengenai saiz orbit objek yang mengorbit Matahari, tetapi tidak memberikan pengukuran skala keseluruhan sistem orbit. Radar digunakan untuk mengukur jarak antara orbit bumi dan jasad kedua. Daripada ukuran dan nisbah kedua-dua saiz orbit, saiz orbit bumi dikira. Orbit bumi diketahui dengan ketepatan mutlak beberapa meter dan ketepatan relatif beberapa 1×10−11.
Secara sejarah, pemerhatian transit Zuhrah adalah penting dalam menentukan AU; pada separuh pertama abad ke-20, pemerhatian asteroid juga penting. Pada masa ini, orbit bumi ditentukan dengan ketepatan tinggi menggunakan pengukuran radar jarak ke Zuhrah dan planet-planet dan asteroid yang berdekatan lain[1], dan dengan mengesan kapal angkasa antara planet dalam orbit mereka mengelilingi Matahari menerusi Sistem Suria.
Paralaks
suntingPengukuran jarak asas yang paling penting berasal dari paralaks trigonometri. Apabila Bumi mengorbit Matahari, kedudukan bintang yang berdekatan akan kelihatan beralih sedikit berbanding belakangnya yang lebih jauh. Peralihan ini adalah sudut dalam segitiga sama kaki, dengan 2 AU (jarak antara kedudukan lampau orbit Bumi keliling Matahari) menjadikan kaki asas segitiga dan jarak ke bintang menjadi kaki yang sama panjang. Jumlah peralihan agak kecil, mengukur 1 arkasaat untuk objek pada jarak 1 parsek (3.26 tahun cahaya) ke bintang yang terdekat, dan selepas itu berkurangan jumlah sudutnya apabila jarak meningkat. Ahli astronomi selalunya menyatakan jarak dalam unit parsek (arkasaat paralaks); tahun cahaya digunakan dalam media popular.
Disebabkan paralaks menjadi lebih kecil untuk jarak yang jauh lebih besar, jarak yang berguna dapat diukur hanya untuk bintang-bintang yang cukup dekat untuk mempunyai paralaks yang lebih besar dari beberapa kali ketepatan pengukuran. Pengukuran paralaks biasanya mempunyai ketepatan yang diukur dalam miliarkasaat.[2] Sebagai contoh, pada 1990-an, misi Hipparcos memperoleh paralaks untuk lebih seratus ribu bintang dengan ketepatan kira-kira satu miliarkasaat,[3] memberikan jarak yang berguna untuk bintang-bintang untuk beberapa ratus parsek. Teleskop Hubble WFC3 kini mempunyai potensi untuk memberikan ketepatan 20 hingga 40 mikroarkasaat, membolehkan pengukuran jarak yang boleh dipercayai sehingga 5,000 parsek (16,000 ly) untuk bilangan kecil bintang.[4][5] Pada tahun 2018, Pelepasan Data 2 dari misi angkasa Gaia memberikan jarak yang sama tepat kepada kebanyakan bintang yang lebih terang daripada magnitud ke-15.[6]
Rujukan
sunting- ^ Ash, M. E.; Shapiro, I. I.; Smith, W. B. (1967). "Astronomical constants and planetary ephemerides deduced from radar and optical observations". The Astronomical Journal. 72: 338. Bibcode:1967AJ.....72..338A. doi:10.1086/110230.
- ^ Staff. "Trigonometric Parallax". The SAO Encyclopedia of Astronomy. Swinburne Centre for Astrophysics and Supercomputing. Dicapai pada 2008-10-18.
- ^ Perryman, M. A. C.; dll. (1999). "The HIPPARCOS Catalogue". Astronomy and Astrophysics. 323: L49–L52. Bibcode:1997A&A...323L..49P.
- ^ Harrington, J. D.; Villard, R. (10 April 2014). "NASA's Hubble Extends Stellar Tape Measure 10 Times Farther Into Space". NASA. Dicapai pada 17 October 2014.
- ^ Riess, A. G.; Casertano, S.; Anderson, J.; MacKenty, J.; Filippenko, A. V. (2014). "Parallax Beyond a Kiloparsec from Spatially Scanning the Wide Field Camera 3 on the Hubble Space Telescope". The Astrophysical Journal. 785 (2): 161. arXiv:1401.0484. Bibcode:2014ApJ...785..161R. doi:10.1088/0004-637X/785/2/161.
- ^ Templat:Cite DR2
Bibliografi
sunting- An Introduction to Modern Astrophysics, Carroll and Ostlie, copyright 2007.
- Measuring the Universe The Cosmological Distance Ladder, Stephen Webb, copyright 2001.
- Pasachoff, JM & Filippenko, AV, The Cosmos: Astronomy in the New Millennium, Cambridge: Cambridge University Press, 4th edition, 2013 ISBN 9781107687561.
- The Astrophysical Journal, The Globular Cluster Luminosity Function as a Distance Indicator: Dynamical Effects, Ostriker and Gnedin, May 5, 1997.
- An Introduction to Distance Measurement in Astronomy, Richard de Grijs, Chichester: John Wiley & Sons, 2011, ISBN 978-0-470-51180-0.